What it’s for:
The F test compares two samples to test the null hypothesis that they have equal variance. This may be of direct interest, but the F test is also often used in conjunction with a t-test. We use a different formula to calculate t if variances are unequal, so before running a t-test we often run an F test. If the null hypothesis is not rejected in the F test, we have no reason to believe the variances of our two populations are different, so we would use the t-test formula assuming equal variance. If the null hypothesis is rejected in the F test, we would use the t-test formula assuming unequal variances.
Assumptions/Cautions:
Test is parametric — data must be normally distributed (Zar 1996).
How to use it:
1) Calculate the variance for each of your samples.
2) Calculate F by dividing the larger variance by the smaller variance, as shown in the box to the right (Zar 1996).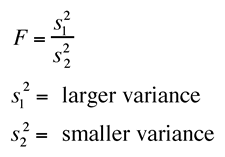
3) Calculate the numerator degrees of freedom as n1-1, where n1 is size of the sample with the larger variance.
4) Calculate the denominator degrees of freedom as n2-1, where n2 is the size of the sample with the smaller variance.
5) Estimate the p-value associated with your F statistic, using a computer program or table.
6) Draw a conclusion, based on the p-value from 5). See also Types of Error.
MS Excel Tips:
MS Excel can calculate the probability associated with your calculated F statistic, using the FDIST function. However, Excel calculates a one-tailed probability. For most uses of the F test, a two-tailed probability is more appropriate (Zar 1996), so you must multiply Excel’s p-value by 2. Excel also has a built-in FTEST function which directly calculates F and the associated probability value from raw data, but this function may misreport F, and is not recommended.
RETURN